[ad_1]
Blockchains are a powerful technology, as regular readers of the blog already likely agree. They allow for a large number of interactions to be codified and carried out in a way that greatly increases reliability, removes business and political risks associated with the process being managed by a central entity, and reduces the need for trust. They create a platform on which applications from different companies and even of different types can run together, allowing for extremely efficient and seamless interaction, and leave an audit trail that anyone can check to make sure that everything is being processed correctly.
However, when I and others talk to companies about building their applications on a blockchain, two primary issues always come up: scalability and privacy. Scalability is a serious problem; current blockchains, processing 3-20 transactions per second, are several orders of mangitude away from the amount of processing power needed to run mainstream payment systems or financial markets, much less decentralized forums or global micropayment platforms for IoT. Fortunately, there are solutions, and we are actively working on implementing a roadmap to making them happen. The other major problem that blockchains have is privacy. As seductive as a blockchain’s other advantages are, neither companies or individuals are particularly keen on publishing all of their information onto a public database that can be arbitrarily read without any restrictions by one’s own government, foreign governments, family members, coworkers and business competitors.
Unlike with scalability, the solutions for privacy are in some cases easier to implement (though in other cases much much harder), many of them compatible with currently existing blockchains, but they are also much less satisfying. It’s much harder to create a “holy grail” technology which allows users to do absolutely everything that they can do right now on a blockchain, but with privacy; instead, developers will in many cases be forced to contend with partial solutions, heuristics and mechanisms that are designed to bring privacy to specific classes of applications.
The Holy Grail
First, let us start off with the technologies that are holy grails, in that they actually do offer the promise of converting arbitrary applications into fully privacy-preserving applications, allowing users to benefit from the security of a blockchain, using a decentralized network to process the transactions, but “encrypting” the data in such a way that even though everything is being computed in plain sight, the underlying “meaning” of the information is completely obfuscated.
The most powerful technology that holds promise in direction is, of course, cryptographically secure obfuscation. In general, obfuscation is a way of turning any program into a “black box” equivalent of the program, in such a way that the program still has the same “internal logic”, and still gives the same outputs for the same inputs, but it’s impossible to determine any other details about how the program works.
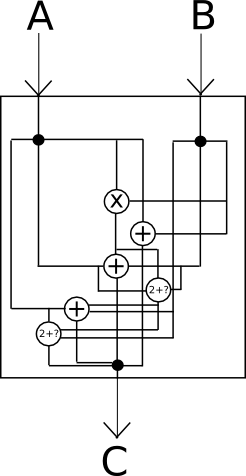
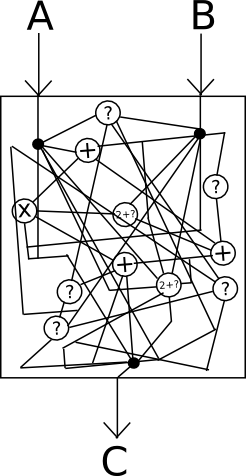
Think of it as “encrypting” the wires inside of the box in such a way that the encryption cancels itself out and ultimately has no effect on the output, but does have the effect of making it absolutely impossible to see what is going on inside.
Unfortunately, absolutely perfect black-box obfuscation is mathematically known to be impossible; it turns out that there is always at least something that you can get extract out of a program by looking at it beyond just the outputs that it gives on a specific set of inputs. However, there is a weaker standard called indistinguishability obfuscation that we can satisfy: essentially, given two equivalent programs that have been obfuscated using the algorithm (eg. x = (a + b) * c and x = (a * c) + (b * c)), one cannot determine which of the two outputs came from which original source. To see how this is still powerful enough for our applications, consider the following two programs:
- y = 0
- y = sign(privkey, 0) – sign(privkey, 0)
One just returns zero, and the other uses an internally contained private key to cryptographically sign a message, does that same operation another time, subtracts the (obviously identical) results from each other and returns the result, which is guaranteed to be zero. Even though one program just returns zero, and the other contains and uses a cryptographic private key, if indistinguishability is satisfied then we know that the two obfuscated programs cannot be distinguished from each other, and so someone in possession of the obfuscated program definitely has no way of extracting the private key – otherwise, that would be a way of distinguishing the two programs. That’s some pretty powerful obfuscation right there – and for about two years we’ve known how to do it!
So, how do we use this on a blockchain? Here’s one simple approach for a digital token. We create an obfuscated smart contract which contains a private key, and accepts instructions encrypted with the correponding public key. The contract stores account balances in storage encrypted, and if the contract wants to read the storage it decrypts it internally, and if the contract wants to write to storage it encrypts the desired result before writing it. If someone wants to read a balance of their account, then they encode that request as a transaction, and simulate it on their own machine; the obfuscated smart contract code will check the signature on the transaction to see if that user is entitled to read the balance, and if they are entitled to read the balance it will return the decrypted balance; otherwise the code will return an error, and the user has no way of extracting the information.
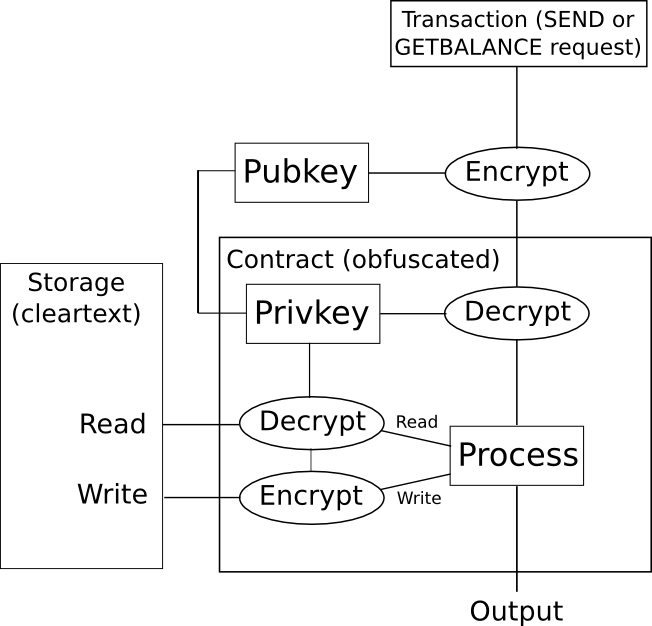
However, as with several other technologies of this type, there is one problem: the mechanism for doing this kind of obfuscation is horrendously inefficient. Billion-factor overhead is the norm, and often even highly optimistic; a recent paper estimates that “executing [a 2-bit multiplication] circuit on the same CPU would take 1.3 * 108 years”. Additionally, if you want to prevent reads and writes to storage from being a data leak vector, you must also set up the contract so that read and write operations always modify large portions of a contract’s entire state – another source of overhead. When, on top of that, you have the overhead of hundreds of nodes running the code on a blockchain, one can quickly see how this technology is, unfortunately, not going to change anything any time soon.
Taking A Step Down
However, there are two branches of technology that can get you almost as far as obfuscation, though with important compromises to the security model. The first is secure multi-party computation. Secure multi-party computation allows for a program (and its state) to be split among N parties in such a way that you need M of them (eg. N = 9, M = 5) to cooperate in order to either complete the computation or reveal any internal data in the program or the state. Thus, if you can trust the majority of the participants to be honest, the scheme is as good as obfuscation. If you can’t, then it’s worthless.
The math behind secure multi-party computation is complex, but much simpler than obfuscation; if you are interested in the technical details, then you can read more here (and also the paper of Enigma, a project that seeks to actually implement the secret sharing DAO concept, here). SMPC is also much more efficient than obfuscation, the point that you can carry out practical computations with it, but even still the inefficiencies are very large. Addition operations can be processed fairly quickly, but every time an SMPC instance performs some very small fixed number of multiplication operations it needs to perform a “degree reduction” step involving messages being sent from every node to every node in the network. Recent work reduces the communication overhead from quadratic to linear, but even still every multiplication operation brings a certain unavoidable level of network latency.
The requirement of trust on the participants is also an onerous one; note that, as is the case with many other applications, the participants have the ability to save the data and then collude to uncover at any future point in history. Additionally, it is impossible to tell that they have done this, and so it is impossible to incentivize the participants to maintain the system’s privacy; for this reason, secure multi-party computation is arguably much more suited to private blockchains, where incentives can come from outside the protocol, than public chains.
Another kind of technology that has very powerful properties is zero-knowledge proofs, and specifically the recent developments in “succinct arguments of knowledge” (SNARKs). Zero-knowledge proofs allow a user to construct a mathematical proof that a given program, when executed on some (possibly hidden) input known by the user, has a particular (publicly known) output, without revealing any other information. There are many specialized types of zero-knowledge proofs that are fairly easy to implement; for example, you can think of a digital signature as a kind of zero-knowledge proof showing that you know the value of a private key which, when processed using a standard algorithm, can be converted into a particular public key. ZK-SNARKs, on the other hand, allow you to make such a proof for any function.
First, let us go through some specific examples. One natural use case for the technology is in identity systems. For example, suppose that you want to prove to a system that you are (i) a citizen of a given country, and (ii) over 19 years old. Suppose that your government is technologically progressive, and issues cryptographically signed digital passports, which include a person’s name and date of birth as well as a private and public key. You would construct a function which takes a digital passport and a signature signed by the private key in the passport as input, and outputs 1 if both (i) the date of birth is before 1996, (ii) the passport was signed with the government’s public key, and (iii) the signature is correct, and outputs 0 otherwise. You would then make a zero-knowledge proof showing that you have an input that, when passed through this function, returns 1, and sign the proof with another private key that you want to use for your future interactions with this service. The service would verify the proof, and if the proof is correct it would accept messages signed with your private key as valid.
You could also use the same scheme to verify more complex claims, like “I am a citizen of this country, and my ID number is not in this set of ID numbers that have already been used”, or “I have had favorable reviews from some merchants after purchasing at least $10,000 worth of products from them”, or “I hold assets worth at least $250,000”.
Another category of use cases for the technology is digital token ownership. In order to have a functioning digital token system, you do not strictly need to have visible accounts and balances; in fact, all that you need is a way to solve the “double spending” problem – if you have 100 units of an asset, you should be able to spend those 100 units once, but not twice. With zero-knowledge proofs, we can of course do this; the claim that you would zero-knowledge-prove is something like “I know a secret number behind one of the accounts in this set of accounts that have been created, and it does not match any of the secret numbers that have already been revealed”. Accounts in this scheme become one-time-use: an “account” is created every time assets are sent, and the sender account is completely consumed. If you do not want to completely consume a given account, then you must simply create two accounts, one controlled by the recipient and the other with the remaining “change” controlled by the sender themselves. This is essentially the scheme used by Zcash (see more about how it works here).
For two-party smart contracts (eg. think of something like a financial derivative contract negotiated between two parties), the application of zero-knowledge-proofs is fairly easy to understand. When the contract is first negotiated, instead of creating a smart contract containing the actual formula by which the funds will eventually be released (eg. in a binary option, the formula would be “if index I as released by some data source is greater than X, send everything to A, otherwise send everything to B”), create a contract containing the hash of the formula. When the contract is to be closed, either party can themselves compute the amount that A and B should receive, and provide the result alongside a zero-knowledge-proof that a formula with the correct hash provides that result. The blockchain finds out how much A and B each put in, and how much they get out, but not why they put in or get out that amount.
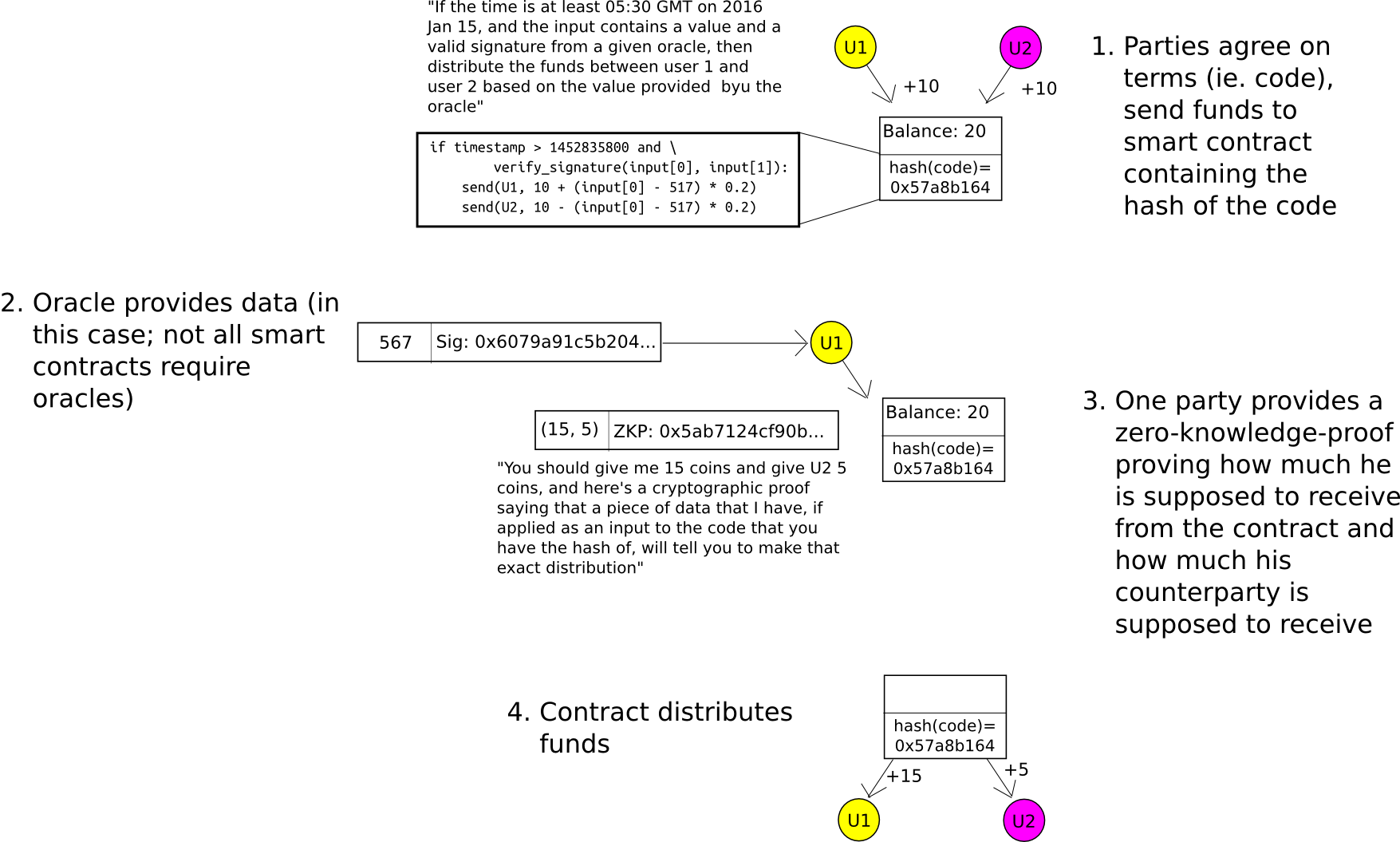
This model can be generalized to N-party smart contracts, and the Hawk project is seeking to do exactly that.
Starting from the Other End: Low-Tech Approaches
The other path to take when trying to increase privacy on the blockchain is to start with very low-tech approaches, using no crypto beyond simple hashing, encryption and public key cryptography. This is the path that Bitcoin started from in 2009; though the level of privacy that it provides in practice is quite difficult to quantify and limited, it still clearly provided some value.
The simplest step that Bitcoin took to somewhat increase privacy is its use of one-time accounts, similar to Zcash, in order to store funds. Just like with Zcash, every transaction must completely empty one or more accounts, and create one or more new accounts, and it is recommended for users to generate a new private key for every new account that they intend to receive funds into (though it is possible to have multiple accounts with the same private key). The main benefit that this brings is that a user’s funds are not linked to each other by default: if you receive 50 coins from source A and 50 coins from source B, there is no way for other users to tell that those funds belong to the same person. Additionally, if you spend 13 coins to someone else’s account C, and thereby create a fourth account D where you send the remaining 37 coins from one of these accounts as “change”, the other users cannot even tell which of the two outputs of the transaction is the “payment” and which is the “change”.

However, there is a problem. If, at any point in the future, you make a transaction consuming from two accounts at the same time, then you irrevertibly “link” those accounts, making it obvious to the world that they come from one user. And, what’s more, these linkages are transitive: if, at any point, you link together A and B, and then at any other point link together A and C, and so forth, then you’ve created a large amount of evidence by which statistical analysis can link up your entire set of assets.

Bitcoin developer Mike Hearn came up with a mitigation strategy that reduces the likelihood of this happening called merge avoidance: essentially, a fancy term for trying really really hard to minimize the number of times that you link accounts together by spending from them at the same time. This definitely helps, but even still, privacy inside of the Bitcoin system has proven to be highly porous and heuristic, with nothing even close to approaching high guarantees.
A somewhat more advanced technique is called CoinJoin. Essentially, the CoinJoin protocol works as follows:
- N parties come together over some anonymous channel, eg. Tor. They each provide a destination address D[1] … D[N].
- One of the parties creates a transaction which sends one coin to each destination address.
- The N parties log out and then separately log in to the channel, and each contribute one coin to the account that the funds will be paid out from.
- If N coins are paid into the account, they are distributed to the destination addresses, otherwise they are refunded.
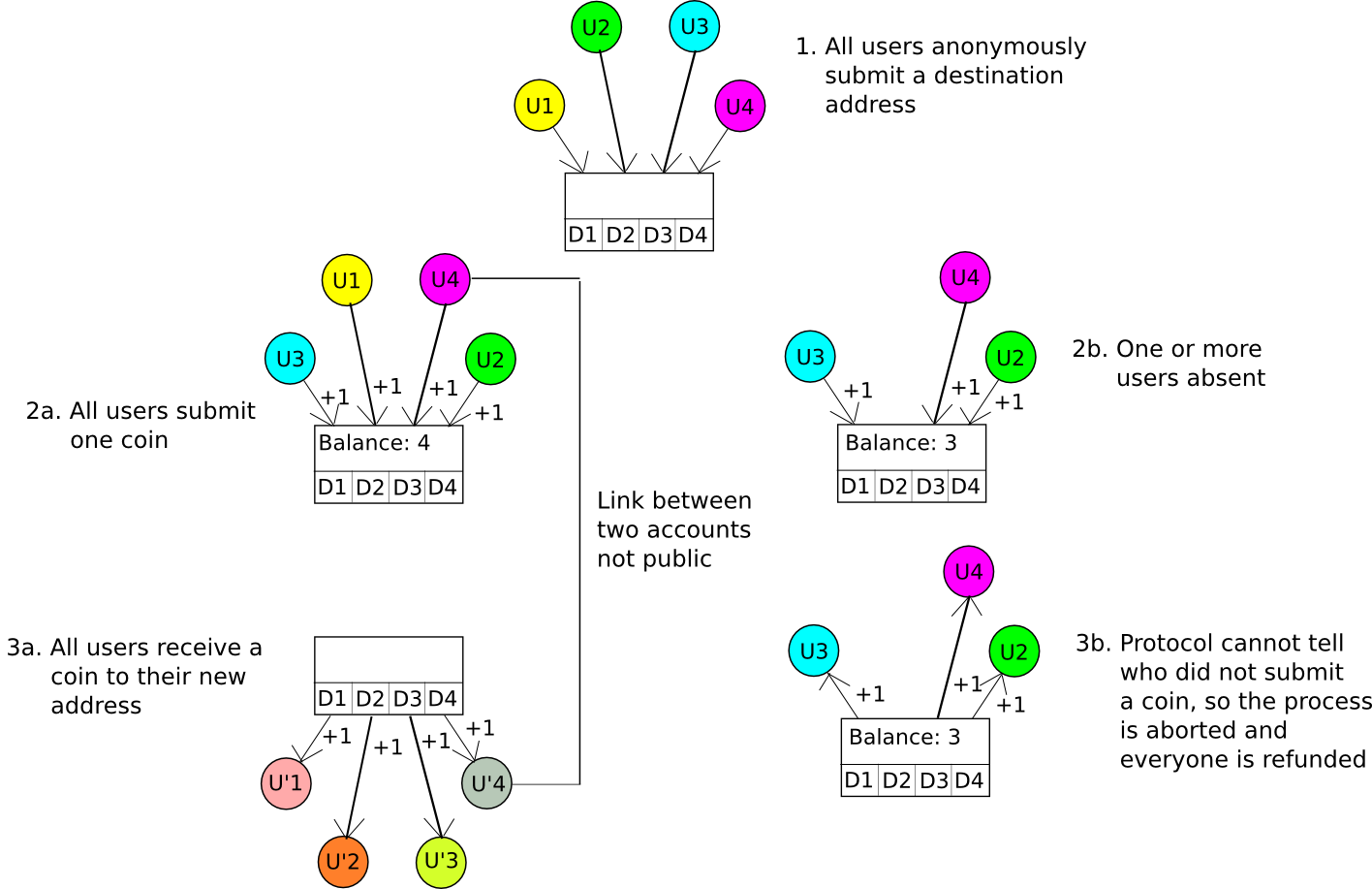
If all participants are honest and provide one coin, then everyone will put one coin in and get one coin out, but no one will know which input maps to which output. If at least one participant does not put one coin in, then the process will fail, the coins will get refunded, and all of the participants can try again. An algorithm similar to this was implemented by Amir Taaki and Pablo Martin for Bitcoin, and by Gavin Wood and Vlad Gluhovsky for Ethereum.
So far, we have only discussed token anonymization. What about two-party smart contracts? Here, we use the same mechanism as Hawk, except we substitute the cryptography with simpler cryptoeconomics – namely, the “auditable computation” trick. The participants send their funds into a contract which stores the hash of the code. When it comes time to send out funds, either party can submit the result. The other party can either send a transaction to agree on the result, allowing the funds to be sent, or it can publish the actual code to the contract, at which point the code will run and distribute the funds correctly. A security deposit can be used to incentivize the parties to participate honestly. Hence, the system is private by default, and only if there is a dispute does any information get leaked to the outside world.
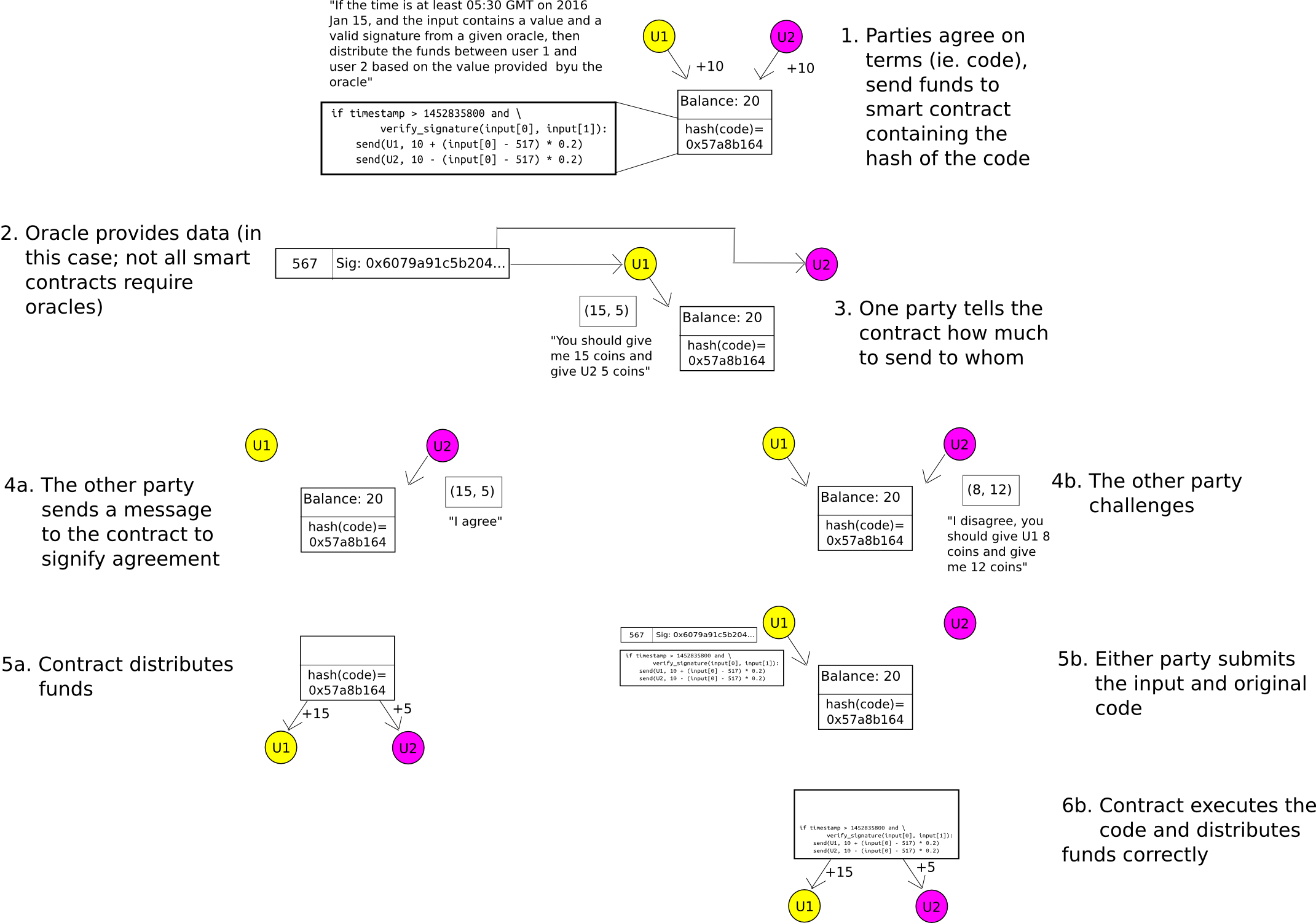
A generalization of this technique is called state channels, and also has scalability benefits alongside its improvements in privacy.
Ring Signatures
A technology which is moderately technically complicated, but extremely promising for both token anonymization and identity applications, is ring signatures. A ring signature is essentially a signature that proves that the signer has a private key corresponding to one of a specific set of public keys, without revealing which one. The two-sentence explanation for how this works mathematically is that a ring signature algorithm includes a mathematical function which can be computed normally with just a public key, but where knowing the private key allows you to add a seed to the input to make the output be whatever specific value you want. The signature itself consists of a list of values, where each value is set to the function applied to the previous value (plus some seed); producing a valid signature requires using knowledge of a private key to “close the loop”, forcing the last value that you compute to equal the first. Given a valid “ring” produced in this way, anyone can verify that it is indeed a “ring”, so each value is equal to the function computed on the previous value plus the given seed, but there is no way to tell at which “link” in the ring a private key was used.
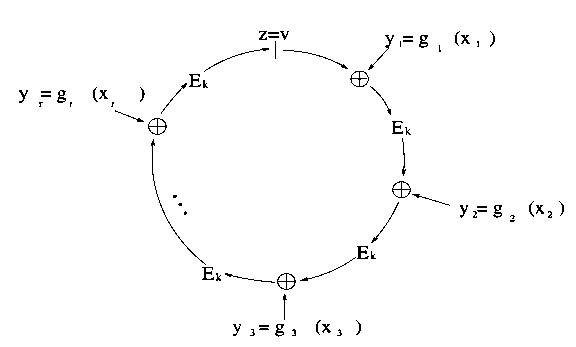
There is also an upgraded version of a ring signature called a linkable ring signature, which adds an extra property: if you sign twice with the same private key, that fact can be detected – but no other information is revealed. In the case of token anonymization, the application is fairly simple: when a user wants to spend a coin, instead of having them provide a regular signature to prove ownership of their public key directly, we combine public keys together into groups, and ask the user to simply prove membership in the group. Because of the linkability property, a user that has one public key in a group can only spend from that group once; conflicting signatures are rejected.
Ring signatures can also be used for voting applications: instead of using ring signatures to validate spending from a set of coins, we use them to validate votes. They can also be used for identity applications: if you want to prove that you belong to a set of authorized users, without revealing which one, ring signatures are well-suited for just that. Ring signatures are more mathematically involved than simple signatures, but they are quite practical to implement; some sample code for ring signatures on top of Ethereum can be found here.
Secret Sharing and Encryption
Sometimes, blockchain applications are not trying to mediate the transfer of digital assets, or record identity information, or process smart contracts, and are instead being used on more data-centric applications: timestamping, high-value data storage, proof of existence (or proof of inexistence, as in the case of certificate revocations), etc. A common refrain is the idea of using blockchains to build systems where “users are in control of their own data”.
In these cases, it is once again important to note that blockchains do NOT solve privacy issues, and are an authenticity solution only. Hence, putting medical records in plaintext onto a blockchain is a Very Bad Idea. However, they can be combined with other technologies that do offer privacy in order to create a holistic solution for many industries that does accomplish the desired goals, with blockchains being a vendor-neutral platform where some data can be stored in order to provide authenticity guarantees.
So what are these privacy-preserving technologies? Well, in the case of simple data storage (eg. medical records), we can just use the simplest and oldest one of all: encryption! Documents that are hashed on the blockchain can first be encrypted, so even if the data is stored on something like IPFS only the user with their own private key can see the documents. If a user wants to grant someone else the right to view some specific records in decrypted form, but not all of them, one can use something like a deterministic wallet to derive a different key for each document.
Another useful technology is secret sharing (described in more detail here), allowing a user to encrypt a piece of data in such a way that M of a given N users (eg. M = 5, N = 9) can cooperate to decrypt the data, but no fewer.
The Future of Privacy
There are two major challenges with privacy preserving protocols in blockchains. One of the challenges is statistical: in order for any privacy-preserving scheme to be computationally practical, the scheme must only alter a small part of the blockchain state with every transaction. However, even if the contents of the alteration are privacy, there will inevitably be some amount of metadata that is not. Hence, statistical analyses will always be able to figure out something; at the least, they will be able to fish for patterns of when transactions take place, and in many cases they will be able to narrow down identities and figure out who interacts with whom.
The second challenge is the developer experience challenge. Turing-complete blockchains work very well for developers because they are very friendly to developers that are completely clueless about the underlying mechanics of decentralization: they create a decentralized “world computer” which looks just like a centralized computer, in effect saying “look, developers, you can code what you were planning to code already, except that this new layer at the bottom will now make everything magically decentralized for you”. Of course, the abstraction is not perfect: high transaction fees, high latency, gas and block reorganizations are something new for programmers to contend with, but the barriers are not that large.
With privacy, as we see, there is no such magic bullet. While there are partial solutions for specific use cases, and often these partial solutions offer a high degree of flexibility, the abstractions that they present are quite different from what developers are used to. It’s not trivial to go from “10-line python script that has some code for subtracting X coins from the sender’s balance and adding X coins to the recipient’s balance” to “highly anonymized digital token using linkable ring signatures”.
Projects like Hawk are very welcome steps in the right direction: they offer the promise of converting an arbitrary N-party protocol into a zero-knowledge-ified protocol that trusts only the blockchain for authenticity, and one specific party for privacy: essentially, combining the best of both worlds of a centralized and decentralized approach. Can we go further, and create a protocol that trusts zero parties for privacy? This is still an active research direction, and we’ll just have to wait and see how far we can get.
[ad_2]
Source link